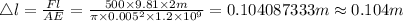Question

Find the elongation produced in a copper wire of length 2m and radius 5mm, when suspended by a block

of mass 500Kg. (Take Young's modulus of elasticity of copper Y = 1,2 ×109 Pa).

Answer 1

0.104 m

Step-by-step explanation:

Stress,
`\sigma=\frac {F}{A}`

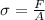
Where F is force and A is area. Also, F=mg where m is mass and g is acceleration due to gravity

`Area= \pi r^(2)`

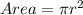
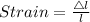`Strain=\frac {\triangle l}{l}` where
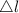`\triangle l` is the elongation and l is the original length

`E=\frac {stress}{strain}=\frac {\frac {F}{A}}{\frac {\triangle l}{l}}=\frac {Fl}{A\triangle l}`

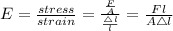
Making
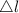`\triangle l` the subject then

`\triangle l=\frac {Fl}{AE}=(mg l)/(\pi r^(2) E)`

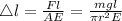
By substituting the given values and taking g as 9.81 then

`\triangle l=\frac {Fl}{AE}=(500* 9.81* 2 m)/(\pi * 0.005^(2)* 1.2* 10^(9))=0.104087333  m\approx 0.104 m`