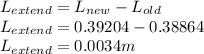Answer:
a.3Hz
b.0.0034m
Step-by-step explanation:
First, we know the flute is an open pipe, because open pipe as both end open and a close organ pipe as only one end close.
The formula relating the length and he frequency is giving as
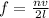 .
.
a.we first determine the length of the flute at the fundamental frequency i.e when n=1 and when the speed is in the 342m/s
Hence from
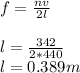 .
.
since the value of the length will remain constant, we now use the value to determine the frequency when the air becomes hotter and the speed becomes 345m/s.

Hence the require beat is
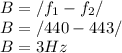 .
.
b. since the length is dependent also on the speed and frequency, we determine the new length when she plays with a fundamental frequency when the speed of sound is 345m/s
using the formula
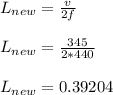
Now to determine the extension,