Question

A wire of diameter d is stretched along the centerline of a pipe of diameter D. For a given pressure drop per unit length of pipe, by how much does the presence of the wire reduce the flow- rate if

(a) d/D = 0.1;
(b) d/D = 0.01?

Answer 1

Part A: (d/D=0.1)

DeltaV percent=42.6%

Part B:(d/D=0.01)

DeltaV percent=21.7%

Step-by-step explanation:

We are going to use the following volume flow rate equation:

`DeltaV=(\pi * DeltaP)/(8*u*l)(R^(4)-r^(4) -((R^(2)-r^(2)))/(ln(R)/(r))^(2))`

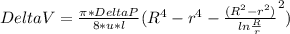
Above equation can be written as:

`DeltaV=(\pi*R^(4)*DeltaP)/(8*u*l)(1-((r)/(R) )^(4)+((1-((r)/(R) )^(2)))/(ln(r)/(R))^(2))`

`DeltaV=(\pi*R^(4)*DeltaP)/(8*u*l)(1-((d)/(D) )^(4)+((1-((d)/(D))^(2)))/(ln(d)/(D))^(2))`

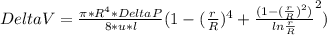
First Consider no wire i.e d/D=0

Above expression will become:

`DeltaV=(\pi*R^(4)*DeltaP)/(8*u*l)(1-(0)^(4)+((1-(0)^(2)))/(ln0)^(2))`

`DeltaV=(\pi*R^(4)*DeltaP)/(8*u*l)`

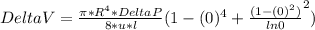
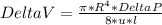
Part A: (d/D=0.1)

`DeltaV=(\pi*R^(4)*DeltaP)/(8*u*l)(1-(0.1)^(4)+((1-(0.1)^(2)))/(ln0.1)^(2))`

`DeltaV=(\pi*R^(4)*DeltaP)/(8*u*l)*0.574`

`DeltaV percent=(((\pi*R^(4)*DeltaP)/(8*u*l))-(\pi *R^(4)*DeltaP)/(8*u*l)*0.574)/((\pi*R^(4)*DeltaP)/(8*u*l) )*100`

`DeltaV percent=(1-0.574)/(1)*100`

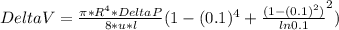
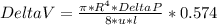
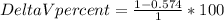
DeltaV percent=42.6%

Part B:(d/D=0.01)

`DeltaV=(\pi*R^(4)*DeltaP)/(8*u*l)(1-(0.01)^(4)+((1-(0.01 )^(2)))/(ln0.01)^(2))`

`DeltaV=(\pi*R^(4)*DeltaP)/(8*u*l)*0.783`

`DeltaV percent=(((\pi *R^(4)*DeltaP)/(8*u*l))-(\pi *R^(4)*DeltaP)/(8*u*l)*0.783)/((\pi *R^(4)*DeltaP)/(8*u*l) )*100`

`DeltaV percent=(1-0.783)/(1)*100`

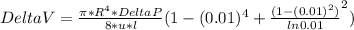
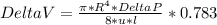
DeltaV percent=21.7%