Answer:
c. (0.248, 0.392)
Explanation:
We have a large simple random sample of n = 400 people and 128 of them know how to ski. Let p be the true proportion of people in the city who know how to ski, then
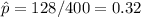 is an estimated of p. An approximation of the standard deviation of
is an estimated of p. An approximation of the standard deviation of
 is
is
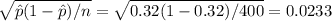 . Because we want a 99.8% confidence interval for the proportion of people in the city who know how to ski, we have that
. Because we want a 99.8% confidence interval for the proportion of people in the city who know how to ski, we have that
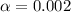 , we need
, we need
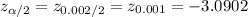 , i.e., the 0.1th quantile of the standard normal distribution. Therefore, the 99.8% confidence interval is given by
, i.e., the 0.1th quantile of the standard normal distribution. Therefore, the 99.8% confidence interval is given by
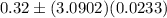 , i.e., (0.2480, 0.3920)
, i.e., (0.2480, 0.3920)