Answer:
- Gap between the plates
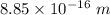
- No, practically not achievable
Solution:
As per the question:
Capacitance, C = 1 F
Area of the plate of the capacitor, A =
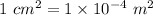
Now,
To calculate the distance, D between the plates of a parallel plate capacitor:
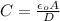
Thus
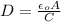
where
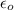 = permittivity of free space
= permittivity of free space
Now,
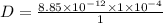
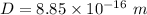
This distance much smaller and is practically not possible