Answer:
The sound energy is
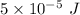 .
.
Step-by-step explanation:
Given that,
Diameter = 7.90 mm
Suppose the intensity for threshold of pain is 1.00 W/m².
We need to calculate the area
Formula of area
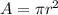
Put the value into the formula
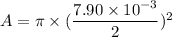
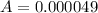
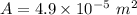
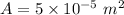
We need to calculate the power
Using formula of power
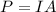
Where, P = Power
I = intensity
A = area
Put the value into the formula
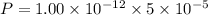
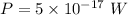
We need to calculate the incident power at the threshold of pain
Using formula of power
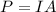

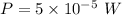
We need to calculate the energy
Using formula of energy
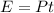
Where. P = power
t = time
Put the value into the formula
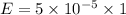
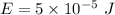
Hence, The sound energy is
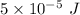 .
.