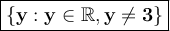Answer:
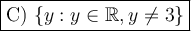
Explanation:
The range is the spread of the y-values (minimum to maximum distance travelled).
The graph of your function is a hyperbola shifted two units left and three units up from the origin.
There is a vertical asymptote at x = -2, so y does not exist when x = -2. However,
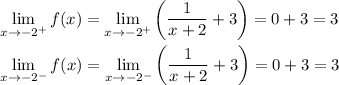
Since the limit from either side is the same,
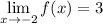
The graph below shows the asymptotes of your function.
Thus. y can take any value except 3.
In set builder notation, the range is