Question

Three equal masses of 3.4 kg each are located at three corners of a square of edge length 2.2 m. Use G = 6.67259 × 10−11 N m2 /kg2 . Find the magnitude of the gravitational field at the fourth corner due to these masses. Answer in units of N/kg.

Answer 1

`g=8.97* 10^(-11)\ N/kg`

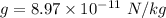
Step-by-step explanation:

It is given that,

Mass of three objects,
`m_1=m_2=m_3=3.4\ kg`

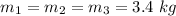
Edge of square, l = 2.2 m

Gravitational constant,
`G=6.67259* 10^(-11)\ Nm^2/kg^2`

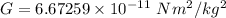
Let g is the magnitude of the gravitational field at the fourth corner due to these masses. It is equal to the sum of magnitude due to diagonal mass and magnitudes due to two neighborhood masses.

`g=(Gm)/((√(2l) )^2)+(Gm√(2) )/(l^2)`

`g=(Gm)/(l^2)((1)/(2)+√(2))`

`g=(6.67259* 10^(-11)* 3.4)/((2.2)^2)((1)/(2)+√(2))`

`g=8.97* 10^(-11)\ N/kg`

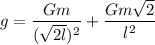
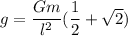
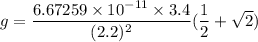
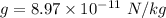
So, the magnitude of the gravitational field at the fourth corner due to these masses is
`8.97* 10^(-11)\ N/kg`. Hence, this is the required solution.