Question

A 0.110-kg cube of ice (frozen water) is floating in glycerine. The glycerine is in a tall cylinder that has an inside radius of 3.70 cm. The level of the glycerine is well below the top of the cylinder.

If the ice completely melts, by what distance does the height of the liquid in the cylinder change?

Answer 1

Δ h = 0.06 m

Step-by-step explanation:

Given,

mass of ice cube = 0.11 Kg

inside radius of cylinder = 3.70 cm

density of water = 1000 Kg/m³

density of glycerin = 1260 Kg/m³

ice cube is floating on glycerin surface,

net force on the cube is equal to zero.

Buoyant force by glycerin is equal to the weight of cube

B = W

`\rho_g V g = m g`

`\rho_g (\pi r^2 h_1)= m`

`h_1= (m)/(\rho_g\pi r^2)`

`h_1= (0.11)/(1260\pi* 0.037^2)`

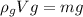
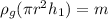
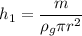
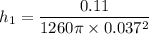
h₁ = 0.0203 m

when ice melts it is completely turned into water

Volume of mass m of water

`V = (m)/(\rho_w)`

`\pi r^2 h_2 = (m)/(\rho_w)`

`h_2 = (m)/(\rho_w\pi r^2)`

`h_2 = (0.11)/(1000\pi* 0.037^2)`

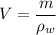
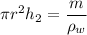
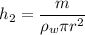
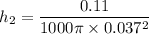
h₂ = 0.0803 m

distance by which height of liquid change

Δ h = h₂ - h₁

Δ h = 0.0803 - 0.0203

Δ h = 0.06 m