Question

At Appalachian State University it is known that 52% of undergraduates are female. If a sample of 150 undergraduate students was taken, which of the following would accurately describe the sampling distribution?

Select all that apply.
Select one or more:

a. The sampling distribution will be approximately normal.
b. The sampling distribution will be skewed right.
c. The sampling distribution will be skewed left. Incorrect
d. The mean of the sampling distribution will be close to 52% Correct
e. The mean of the sampling distribution will be close to 50%
f. We can not determine the mean of the sampling distribution from the given information.
g. The standard deviation of the sampling distribution will be 0.0408
h. The standard deviation of the sampling distribution will be 0.0017 Incorrect
i. The standard deviation of the sampling distribution will be 0.4996.
j. We can not determine the standard deviation of the sampling distribution from the given information.

Answer 1

a. The sampling distribution will be approximately normal.

d. The mean of the sampling distribution will be close to 52%

g. The standard deviation of the sampling distribution will be 0.0408

Explanation:

For this problem the sample size is large enough (n>30), and then the sampling distribution
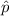`\hat p` would be approximately normal. The mean of the sampling distributions is given by
`p=0.52`

The expected value for the sampling distribution would be 0.52 since
`E(\hat p) = p`

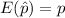
And for the standard deviation we know that is given by:

`Sd= \sqrt{(p (1-p))/(n)}=\sqrt{(0.52(1-0.52))/(150)}=0.0408`

So the correct answers on this case are:

a. The sampling distribution will be approximately normal.

d. The mean of the sampling distribution will be close to 52%

g. The standard deviation of the sampling distribution will be 0.0408