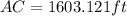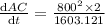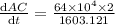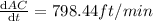Answer:
Explanation:
Velocity of first Person
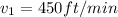
Velocity of second Person
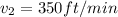
Distance between them P=100 ft
Let x be the distance moved by 1 st and y be the distance moved by second person by the time 12:02 PM
In Triangle ABC
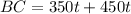
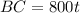
using Pythagoras
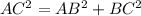
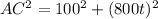
differentiating with respect to time
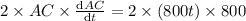
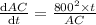
AC after 2 minute