Question

A person wears a hearing aid that uniformly increases the sound level of all audible frequencies of sound by 28.1 dB. The hearing aid picks up sound having a frequency of 250 Hz at an intensity of 3.30 10-11 W/m2. What is the intensity delivered to the eardrum?

Answer 1

I₂ = 2.13 x 10⁻⁸ W/m²

Step-by-step explanation:

given,

increase in sound level = 28.1 dB

frequency of the sound = 250 Hz

intensity = 3.3 x 10⁻¹¹ W/m²

Intensity delivered = ?

the difference of intensity level is give as

`\beta_2-\beta_1 = 10log((I_2)/(I_o)) - 10log((I_1)/(I_o))`

`\beta_2-\beta_1 = 10(log((I_2)/(I_o)) -log((I_1)/(I_o)))`

`\beta_2-\beta_1 = 10(log((I_2)/(I_1))`

`28.1= 10(log((I_2)/(I_1))`

`log(I_2)/(I_1)=2.81`

`(I_2)/(I_1)=10^(2.81)`

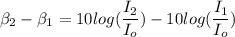
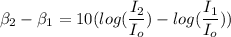
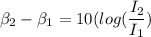
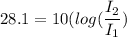
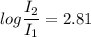
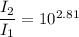
I₂ = 645.65 I₁

I₂ = 645.65 x 3.3 x 10⁻¹¹

I₂ = 2.13 x 10⁻⁸ W/m²