Question

Use the sample data to construct a 95​% confidence interval estimate of the percentage of cell phone users who develop cancer of the brain or nervous system.

Answer 1

The sample data to construct a 95% confidence interval estimate of the percentage of cell phone users who develop cancer of the brain or nervous system.

0.000267 % ∠p ∠0.000375%

A range of values that, with a particular level of confidence, is likely to encompass a population value is called a confidence interval. A population mean is typically stated as a percentage that falls between an upper and lower interval.

The range of values in a confidence interval below and above the sample statistic is called the margin of error.

The normal distribution is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

The distribution of the population proportion is as follows:

p ≈ N
`(N, \sqrt{(p(1-p))/(n) } )`

Since we are determining the interval for a proportion, we must consider this while determining the crucial value. In this instance, the z distribution must be used. Given the 95% confidence level of our interval, our significance level would be determined by

α = 1- 0.95 = 0.05

`(\alpha)/(2) = 0.25`

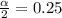
Critical value ,

`Z_{(\alpha)/(2) }` = -1.96

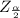`Z_1_{(-\alpha)/(2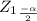) }` = 1.96

To find the confidence interval We have to use the formula:

`\bar p` ±
`Z_{(\alpha)/(2) }\sqrt{(\bar p(1-\bar p))/(n) }`

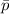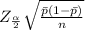
Substitute the value in this formula

0.000321 ± 1.96
`\sqrt{(0.000321 (1-0.000321))/(4200095) }`

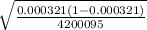
After solving these we get interval as

= (0.000267 ; 0.000375)

That means

The value of p is greater than 0.000267 and less than 0.000375.

Question:-

A study of 420,023 cell phone users found that 134 of them developed cancer of the brain or nervous system. Prior to this study of cell phone use, the rate of such cancer was found to be 0.0323% for those not using cell phones.

Complete part: Use the sample data to construct a 95% confidence interval estimate of the percentage of cell phone users who develop cancer of the brain or nervous system.

__ % ∠p ∠__%

Answer 2

The 95% confidence interval would be given by (0.000267;0.000375)

Explanation:

Assuming this problem: "Use the data and confidence level to construct a confidence interval estimate of p, then address the given question. A study of 420,095 Danish cell phone users found that 0.0321 % of them developed cancer of the brain or nervous system. Prior to this study of cell phone use, the rate of such cancer was found to be 0.0340% for those not using cell phones. The data are from the Journal of the National Cancer Institute. Use the sample data to construct a 95% confidence interval estimate of the percentage of cell phone users who develop cancer of the brain or nervous system."

A confidence interval is "a range of values that’s likely to include a population value with a certain degree of confidence. It is often expressed a % whereby a population means lies between an upper and lower interval".

Previous concepts

The margin of error is the range of values below and above the sample statistic in a confidence interval.

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

The population proportion have the following distribution

`p \sim N(p,\sqrt{(p(1-p))/(n)})`

`n=420095` random sample taken

`\hat p=0.000321` estimated proportion of cell phone users who develop cancer of the brain or nervous system.

`p` true population proportion of cell phone users who develop cancer of the brain or nervous system.

Solution to the problem

In order to find the critical value we need to take in count that we are finding the interval for a proportion, so on this case we need to use the z distribution. Since our interval is at 95% of confidence, our significance level would be given by
`\alpha=1-0.95=0.05` and
`\alpha/2 =0.025`. And the critical value would be given by:

`z_(\alpha/2)=-1.96, z_(1-\alpha/2)=1.96`

The confidence interval for the mean is given by the following formula:

`\hat p \pm z_(\alpha/2)\sqrt{(\hat p (1-\hat p))/(n)}`

If we replace the values obtained we got:

`0.000321 - 1.96\sqrt{(0.000321(1-0.000321))/(420095)}=0.000267`

`0.000321 + 1.96\sqrt{(0.000321(1-0.000321))/(420095)}=0.000375`

The 95% confidence interval would be given by (0.000267;0.000375)