Answer:

Explanation:
We are given the following information in the question:
Percentage of of the diners who make reservations don't show up = 3%
Number of reservations = 83
Thus, we are given a binomial distribution with n = 83 and p = 0.97
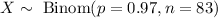
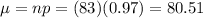
Around 81 people can be expected to show up.
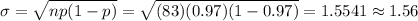
The standard deviation of this distribution is 1.56