Question

Suppose a certain type of fertilizer has an expected yield per acre of mu 1 with variance sigma 2, whereas the expected yield for a second type of fertilizer is mu 2 with the same variance sigma 2. Let S1^2 and S2^2 denote the sample variances of yields based on sample sizes n1 and n2, respectively, of the two fertilizers. Show that the pooled (combined) estimator Cap sigma 2 = (n1 - 1)S1^2 + (n2 - 1)S2^2/n1 + n2 - 2 is an unbiased estimator of sigma 2.

Answer 1

See the proof below.

Explanation:

For this case we just need to apply properties of expected value. We know that the estimator is given by:

`S^2_p= ((n_1 -1) S^2_1 +(n_2 -1) S^2_2)/(n_1 +n_2 -2)`

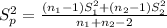
And we want to proof that
`E(S^2_p)= \sigma^2`

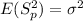
So we can begin with this:

`E(S^2_p)= E(((n_1 -1) S^2_1 +(n_2 -1) S^2_2)/(n_1 +n_2 -2))`

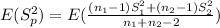
And we can distribute the expected value into the temrs like this:

`E(S^2_p)= ((n_1 -1) E(S^2_1) +(n_2 -1) E(S^2_2))/(n_1 +n_2 -2)`

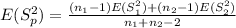
And we know that the expected value for the estimator of the variance s is
`\sigma`, or in other way
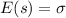`E(s) = \sigma` so if we apply this property here we have:

`E(S^2_p)= ((n_1 -1 )\sigma^2_1 +(n_2 -1) \sigma^2_2)/(n_1 +n_2 -2)`

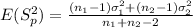
And we know that
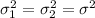`\sigma^2_1 = \sigma^2_2 = \sigma^2` so using this we can take common factor like this:

`E(S^2_p)= ((n_1 -1) +(n_2 -1))/(n_1 +n_2 -2) \sigma^2 =\sigma^2`

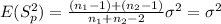
And then we see that the pooled variance is an unbiased estimator for the population variance when we have two population with the same variance.