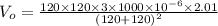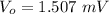Answer:
Output voltage is 1.507 mV
Solution:
As per the question:
Nominal resistance, R =
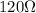
Fixed resistance, R =
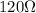
Gauge Factor, G.F = 2.01
Supply Voltage,
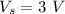
Strain,
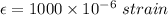
Now,
To calculate the output voltage,
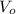 :
:
WE know that strain is given by:
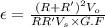
Thus
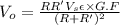
Now, substituting the suitable values in the above eqn: