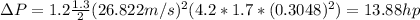Question

A rectangular car-top carrier of 1.7-ft height, 5.0-ft length (front to back), and 4.2-ft width is attached to the top of a car. Estimate the additional power required to drive the car with the carrier at 60 mph through still air compared with the power required to driving only the car at 60 mph. Assume that CD.

Answer 1

`\Delta P =1.2 (1.3)/(2)(26.822m/s)^2 (4.2*1.7*(0.3048)^2)=13.88 hp`

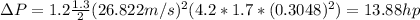
Step-by-step explanation:

We can assume that the general formula for the drag force is given by:

`D= C_D (\rho)/(2)V^2 A`

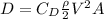
And we can see that is proportional to the area. On this case we can calculate the area with the product of the width and the height. And we can express the grad force like this:

`D_1 = C_(D1) (\rho)/(2)V^2 (wh)`

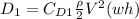
Where w is the width and h the height.

The last formula is without consider the area of the carrier, but if we use the area for the carrier we got:

`D_2 = C_(D2) (\rho)/(2)V^2 (wh+ A_(carrier))`

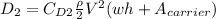
If we want to find the additional power added with the carrier we just need to take the difference between the multiplication of drag force by the velocity (assuming equal velocities for both cases) of the two cases, and we got:

`\Delta P = C_(D2) (\rho)/(2)V^2 (wh+ A_(carrier)) V-  C_(D1) (\rho)/(2)V^2 (wh) V`

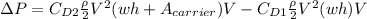
We can assume the same drag coeeficient
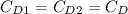`C_(D1)=C_(D2)=C_(D)` and we got:

`\Delta P = C_(D) (\rho)/(2)V^2 (wh+ A_(carrier)) V-  C_(D) (\rho)/(2)V^2 (wh) V`

`\Delta P = C_(D) (\rho)/(2)V^3 (A_(carrier))`

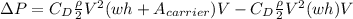
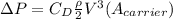
1.7 ft =0.518 m

60 mph = 26.822 m/s

In order to find the drag coeffcient we ned to estimate the Reynolds number first like this:

`R_E= (Vl)/(v)= (26.822m/s*0.518 m)/(1.58x10^(-4) Pa s)= 8.79 x10^(4)`

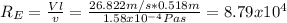
And the value for the kinematic vicosity was obtained from the table of physical properties of the air under standard conditions.

Now we can find the aspect ratio like this:

`(l)/(h)=(5)/(1.7)2.941`

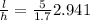
And we can estimate the calue of
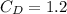`C_D = 1.2` from a figure.

And we can calculate the power difference like this:

`\Delta P =1.2 (1.3)/(2)(26.822m/s)^2 (4.2*1.7*(0.3048)^2)=13.88 hp`