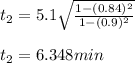Question

An observer moving toward Earth with a speed of 0.84 c notices that it takes 5.1 min for a person to fill her car with gas. Suppose, instead, that the observer had been moving away from Earth with a speed of 0.90 c.

How much time would the observer have measured for the car to be filled in this case?

Answer 1

t₂=6.35min

Step-by-step explanation:

t₁ = first observed time (=5.1 min)

t₂ = unknown; this is the quantity we want to find

V₁ = observer's initial speed (=0.84c)

V₂ = observer's final speed (=0.90c)

Lorentz factors for V₁ and V₂:

γ₁ = 1/√(1−(V₁/c)²)

γ₂ = 1/√(1−(V₂/c)²)

The "proper time" (the time measured by the person filling her car) is:

t′ = t₁/γ₁

The proper time is stated to be the same for both observations, so we also have:

t′ = t₂/γ₂

Combine those two equations and solve for t₂

t₂ = t₁(γ₂/γ₁)

t₂= t₁√((1−(V₁/c)²)/(1−(V₂/c)²))

`t_(2)=5.1\sqrt{(1-(0.84)^(2) )/(1-(0.9)^(2) ) }\\\\t_(2)=6.348min`