Question

An unknown weak acid, HA, it titrated with 1.2 M NaOH. The pH at the halfway point of this titration was found to be 4.102. If the initial pH of the weak acid solution (before titration) has a pH of 2.308, what was the concentration of the weak acid solution?

Answer 1

0.311 M

Step-by-step explanation:

HA, our weak acid, reacts with NaOH by the following equation given below:

`HA (aq) + NaOH (aq)\rightarrow NaA (aq) + H_2O (l)`

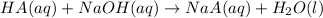
This may also be represented by the net ionic equation for this acid-base reaction:

`HA (aq) + OH^- (aq)\rightarrow A^- (aq) + H_2O (l)`

During the titration up to the equivalence point, we would have some HA remaining and some
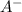`A^-` produced. That said, we have a weak acid and its conjugate base forming a buffer. We may apply the Henderson-Hasselbach equation for buffers here:

`pH = pK_a + log(([A^-])/([HA))`

At midpoint, half of HA reacts to produce half of
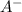`A^-`, meaning
`[HA] = [A^-]` when half of equivalence volume of NaOH is added.

This implies that:

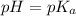`pH = pK_a` at midpoint. We may then find the acid ionization constant for this acid:

`K_a = 10^(-pH) = 10^(-4.102) = 7.91\cdot 10^(-5)`

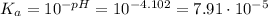
The initial molarity has to be found now. We know that the initial pH is:

`pH = 2.308`

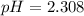
Since
`pH = -log[H_3O^+]`, then
`[H_3O^+] = 10^(-pH)`

Using an ICE table, for some initial molarity of acid,
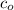`c_o`, we may write the equilibrium constant expression as:

`K_a = ([H_3O^+]^2)/(c_o - [H_3O^+])`

Solve for the initial molarity of HA:

`c_o = ([H_3O^+]^2)/(K_a) + [H_3O^+] = (10^(-2pH))/(K_a) + 10^(-pH) = (10^(-2\cdot 2.308))/(7.91\cdot 10^(-5)) + 10^(-2.308) = 0.311 M`