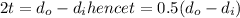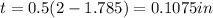Answer:
(a) 2.5 ksi
(b) 0.1075 in
Step-by-step explanation:
(a)
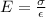
Making
 the subject then
the subject then
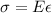
where
 is the stress and
is the stress and
 is the strain
is the strain
Since strain is given as 0.025% of the length then strain is
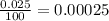
Now substituting E for
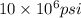 then
then
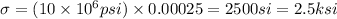
(b)
Stress,
 making A the subject then
making A the subject then
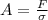
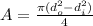
where d is the diameter and subscripts o and i denote outer and inner respectively.
We know that
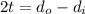 where t is thickness
where t is thickness
Now substituting
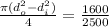
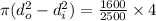
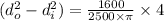
But the outer diameter is given as 2 in hence
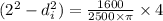
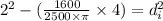
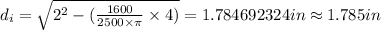
As already mentioned,