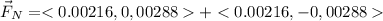Question

Figure 3

b. What is the net electrostatic force on charge due to gi and q2, we
and 92 -5.0 C and they are placed as shown in Figure 4. Take O. =* 2.0 uc,
(10 Marks)
und 2
4.0 m
3.0 m
3.0 m
3,00)
ac

Answer 1

`\vec F_N=<0.00432 , 0>`

Step-by-step explanation:

Electrostatic Forces

When two point charges
`q_1` and
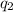`q_2` are placed nearby at a distance r, they exert a force to each other which magnitude can be computed by the Coulomb's formula

`\displaystyle F=(k\ q_1\ q_2)/(r^2)`

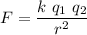
Where k is the constant of proportionality

`k=9.10^9\ Nw.m^2/c^2`

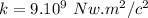
Two positive or negative charges repel each other, one positive and the other negative attract themselves. when analyzing the effects of multiple charges in one, two, or three dimensions, we must consider the forces as vectors.

The figure provided in the question shows 3 point charges, one
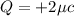`Q=+2\mu c` will receive forces from two charges called
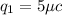`q_1=5\mu c` and
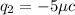`q_2=-5\mu c`. We can see there is some symmetry in the arrangement, which will simplify our calculations

The force
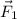`\vec F_1` has components

`\vec F_1=<F_1.cos\theta , F_1.sin\theta>`

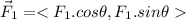
Where
`\theta` is the angle it forms with the positive x-axis. We can see by triangle construction that this angle can be computed by

`\displaystyle sin\theta=(4)/(r)`

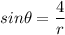
r is the hypotenuse of the triangle formed by the charges, so

`r=√(3^2+4^2)=√(25)=5`

`r=5\ m`

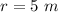
Then, we have

`\displaystyle sin\theta=(4)/(5)=0.8`

`\displaystyle cos\theta=(3)/(5)=0.6`

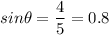
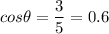
We'll now compute
`F_1`

`\displaystyle F_1=(k\ q_1\ Q)/(r^2)`

`\displaystyle F_1=(9.10^9\ (5.10^(-6))\ (2.10^(-6)))/(25)=0.0036`

`F_1=0.0036\ N`

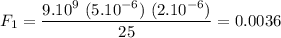
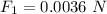
We form the vector

`\vec F_1=<0.0036(0.6) , 0.0036(0.8)>`

`\vec F_1=<0.00216 , 0,00288>\ N`

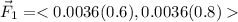
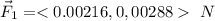
When computing we see some symmetries: The charges
`q_1` and
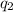`q_2` have the same magnitude and they exert the same force on Q but pointed in another direction. We also note the angle \theta under the horizontal is the same as the one we have found because the right triangle is congruent with the left triangle. The only difference is that the vertical component of
`F_2` points downwards, so

`\vec F_2=<0.00216 , -0,00288>\ N`

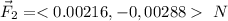
It's clear that the vertical components of the net force will eventually cancel and the net force will be horizontal

`\vec F_N=\vec F_1+\vec F_2`

`\vec F_N=<0.00216 , 0,00288>+<0.00216 , -0,00288>`

`\vec F_N=<0.00432 , 0>`