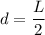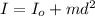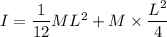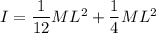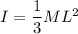Question

The moment of inertia of a uniform thin rod of mass M and length L about an axis through its center and perpendicular to its length is . Find its moment of inertia through through an axis passing through one of its ends and perpendicular to its length.

Answer 1

About center ,
`I_o=(1)/(12)ML^2`

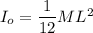
About an end ,
`I=(1)/(3)ML^2`

Step-by-step explanation:

Given that

Mass =m

Length = L

The moment of inertia of rod about center given as

`I_o=(1)/(12)ML^2`

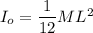
We know that the moment of inertia about a parallel axis which at a distance d from the center given as

I=Io+ m d²

The distance of one end from center

`d=(L)/(2)`

`I=I_o+md^2`

`I=(1)/(12)ML^2+M* (L^2)/(4)`

`I=(1)/(12)ML^2+ (1)/(4)ML^2`

`I=(1)/(3)ML^2`