Question

A 306 g cart moves on a horizontal, frictionless surface with a constant speed of 14.2 cm/s. A 76.3 g piece of modeling clay is dropped vertically onto the cart. If the clay sticks to the cart, find the final speed of the system. Answer in units of cm/s.

Answer 1

To solve this problem it is necessary to apply the concepts related to the conservation of the momentum for an inelastic shock. Mathematically this can be described as

`m_1v_1 + m_2v_2 = (m_1+m_2)V_f`

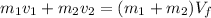
Where,

m_{1,2} = Mass of each object

v_{1,2} = Initial velocity of each object

V_f = Final Velocity

If we assign the value of mass 1 and speed 1 to the cart and the variable of mass 2 to clay (which is at rest) we will have:

`m_1v_1 + m_2v_2 = (m_1+m_2)V_f`

`(306)(14.2) + (76.3)(0) = (306+76.3)V_f`

`V_f = 11.36cm/s`

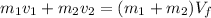
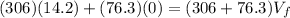
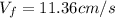
Therefore the final speed of the system would be 11.36cm/s