Answer:

Explanation:
Data given and previous concepts
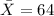 represent the sample mean for the height
represent the sample mean for the height
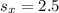 represent the sample deviation for the height
represent the sample deviation for the height
 represent the sample mean for the income
represent the sample mean for the income
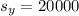 represent the sample deviation for the income
represent the sample deviation for the income
r=0.2 represent the correlation coefficient
The correlation coefficient is a "statistical measure that calculates the strength of the relationship between the relative movements of two variables". It's denoted by r and its always between -1 and 1.
And in order to calculate the correlation coefficient we can use this formula:
![r=(n(\sum xy)-(\sum x)(\sum y))/(√([n\sum x^2 -(\sum x)^2][n\sum y^2 -(\sum y)^2]))](https://img.qammunity.org/2020/formulas/mathematics/middle-school/h2kbdui9ydpsixheffu6h8g6vjzzbhe9ox.png)
Solution to the problem
Let's suppose that we have the following linear model:
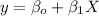
Where Y is the dependent variable (income) and X the independent variable (height).
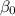 represent the intercept and
represent the intercept and
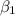 the slope.
the slope.
In order to estimate the coefficients
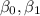 we can use least squares estimation.
we can use least squares estimation.
We have an useful formula in order to estimate the slope for the linear model given by:
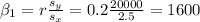
Now we can find the intercept for the linear model with the following formula:
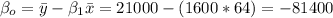
And then our linear model would be given by:

We can estimate the RMS with the following formula:
