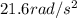Question

Two pulleys are fastened together to form an integral unit. At a certain instant, the indicated belt tensions act on the unit and the unit is turning counterclockwise. Determine the angular acceleration of the unit for this instant if the moment due to friction in the bearing at O is 2.5 N∙m.

Answer 1

α =
`21.6 rad/s^2`

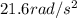
Step-by-step explanation:

Applying the equations of motion to determine angular acceleration of the unit,

The sum of moments about O is equal to the product of angular acceleration and moment of inertia

∑Mo = Io*α

Taking the anticlockwise direction as positive moment,

= ( -(1150) + (1400) ) * (0.5 / 2) + ( (475) - (650) ) * (0.3 / 2) - F = Io*α

= 36.5 - (2.5 N.m) =
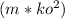`(m*ko^2)`*α

NOTE: moment of inertia of the pulleys in this instance =
`(m*ko^2)`

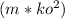
Hence, 33.75 =
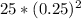`25 * (0.25)^2` * α

Solving, α =
`21.6 rad/s^2`