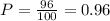Answer:
Explanation:
Given
No of People who can speak English is

No of People who can speak French is

No of People who can speak Spanish is
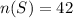
No of People who can speak both English and French
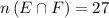
No of People who can speak both English and Spanish
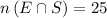
No of People who can speak both French and Spanish
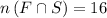
No of people who can speak all languages is
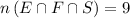
no of People who can Speak at least one Language is
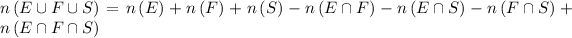
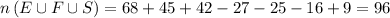
Probability that Randomly selected can speak at least 1 of these languages