Question

The sequence left curly bracket g subscript n right curly bracket is defined recursively as follows: g subscript 0 equals 1 space comma space and space g subscript n equals 3 times g subscript n minus 1 end subscript plus 2 subscript n space comma space for space n greater or equal than 1 . If the theorem below is proven by induction, what must be established in the inductive step?

Answer 1

For all k≥0 if
`g_k=(5)/(2)2^k-k-(3)/(2)` then
`g_(k+1)=(5)/(2)2^(k+1)-(k+1)-(3)/(2)`

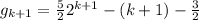
Explanation:

Remember that a proof by induction consists on the following structure:

You want to prove a property p(n) for all natural numbers n.

1. Prove p(0). This is called the base case.
2. Assume that p(k) is true for some natural number (k is an arbitrary natural number; this must hold for all k≥0). With this assumption, prove that p(k+1) is true. This is called the inductive step.

Here, our property is the theorem we want to prove, that is,
`p(k): g_k=(5)/(2)2^k-k-(3)/(2)`.

So, the inductive step "for all k≥0 p(k)→p(k+1)" becomes "for all k≥0 if
`g_k=(5)/(2)2^k-k-(3)/(2)` then
`g_(k+1)=(5)/(2)2^(k+1)-(k+1)-(3)/(2)`"

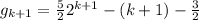If we would want to write the proof, we must use the recursive definition given, in this case,
`g_0=1, g_n=3g_(n-1)+2n`. Notice how this definition and the inductive step are different, but to prove the base case and inductive step you have to use the definition.