Question

In a certain binary-star system, each star has the same mass as our Sun, and they revolve around their center of mass. The distance between them is the same as the distance between Earth and the Sun. What is their period of revolution in years?

Answer 1

T=0.7 [y]

Step-by-step explanation:

The period equation in a circular motion can be written as:

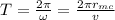`T = (2\pi)/(\omega)=(2\pi r_(mc))/(v)` (1)

where:

• v is the tangential velocity
• T is the period of revolution
• 
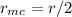  `r_(mc)=r/2` is the distance between the first star and the center of mass.
• r is the distance between two stars

We can find v using the gravitational force equation between two stars:

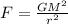`F=(GM^(2))/(r^(2))` (2)

• G is the gravitational constant
• M is the mass of the stars

Now, the force here is just a centripetal force, so
`F = Ma_(c)=Mv^(2)/r_(mc)=2Mv^(2)/r`

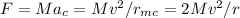
Combining this relation with (2) we have v:

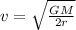`v=\sqrt{(GM)/(2r)}` (3)

Let's put (3) into (1):

`T=\frac{\pi r}{\sqrt{(GM)/(2r)}}`

`T=\sqrt{(2\pi^(2) r^(3))/(GM)}`

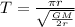
Before finding the period, let's recall some information:

`r=1.5\cdot 10^(11) [m]` (distance between earth and sun)

`M=2.0\cdot 10^(30) [kg]` (solar mass)

`G=6.67\cdot 10^(-11) [m^(3)/kg\cdot s^(2)]` (gravitational constant)

Finally the period in years will be:

`T=\sqrt{(2\pi^(2) r^(3))/(GM)}=2.24\cdot 10^(7) [s]`

`T=0.7 [y]`

Have a nice day!