Question

A sports car starts from rest at an intersection and accelerates toward the east on a straight road at 8.0 m/s2. Just as the sports car starts to move, a bus traveling east at a constant 18 m/s on the same straight road passes the sports car. When the sports car catches up with and passes the bus, (a) how much time has elapsed and (b) how far has the sports car traveled?

Answer 1

The sports car takes 2.25 seconds to catch up with and pass the bus, and it travels a distance of 18 meters.

Step-by-step explanation:

To solve this problem, we need to determine the time it takes for the sports car to catch up with the bus and pass it, as well as the distance the sports car travels.

(a) To find the time, we can use the equation of motion: v = u + at, where v is the final velocity, u is the initial velocity, a is the acceleration, and t is the time.

Since the sports car starts from rest, its initial velocity u = 0 m/s. The bus has a constant velocity of 18 m/s, so we can substitute these values into the equation: 18 = 0 + 8t.

Solving for t, we get: t = 2.25 seconds.

(b) To find the distance the sports car travels, we can use the equation of motion:
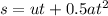`s = ut + 0.5at^2`, where s is the distance traveled. Substituting the values:
`s = 0 + 0.5(8)(2.25)^2.`

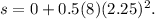
Solving for s, we get: s = 18 meters.

Answer 2

a) t = 4.5 s , b) x = 81 m

Step-by-step explanation:

a) For this problem we will use kinematic relationships

For the car

x = v₀ t + ½ a₁ t²

Since the car kicks from rest, the initial speed is zero

x = ½ a₁ t²

For the bus

v₂ = x / t

x = v₂ t

At the point where they are located it has the same position, so we can match the equation

½ a₁1 t² = v₂ t

½ a₁ t = v₂

t = 2 v₂ / a₁

Let's calculate

t = 2 18 /8.0

t = 4.5 s

b) to find the position

x = v₂ t

x = 18 4.5

x = 81 m