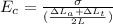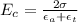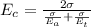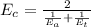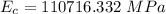Question

Two rods are identical in all respects except one: one rod is made from aluminum (Young's modulus 6.9 x 1010 N/m2), and the other from tungsten (Young's modulus 2.8 x 1011 N/m2). The rods are joined end to end, in order to make a single rod that is twice as long as either the aluminum or tungsten rod. What is the effective value of Young's modulus for this composite rod? That is, what value YComposite of Young's modulus should be used in Equation 10.17 when applied to the composite rod? Note that the change LComposite in the length of the composite rod is the sum of the changes in length of the aluminum and tungsten rods.

Answer 1

`E_c=110716.332\ MPa`

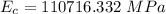
Step-by-step explanation:

Given:

• young's modulus of aluminium,
  `E_a=6.9* 10^4\ MPa`

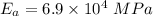
• young's modulus of tungsten,
  `E_t=2.8* 10^5\ MPa`

When the rods are joined in series the the force applied on each rod is equal to the end force on the composite series rod.

Now, equating the forces on the two rods:

`F_a=F_t`

`\sigma_a.A=\sigma_t.A`

`\sigma_a=\sigma_t=\sigma \rm (say)`

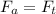
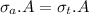
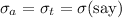
Now, young's modulus for the composite rod:

`E_c=(\sigma)/(\epsilon_c)`

`E_c=(\sigma)/((\Delta L_c)/(2L) )`

`E_c=(\sigma)/(((\Delta L_a+\Delta L_t)/(2L)) )`

`E_c=(\sigma)/((\epsilon_a)/(2)+(\epsilon_t)/(2))`

`E_c=(2\sigma)/(\epsilon_a+\epsilon_t)`

`E_c=(2\sigma)/((\sigma)/(E_a) +(\sigma)/(E_t) )`

`E_c=(2)/((1)/(E_a) +(1)/(E_t) )`

`E_c=(2)/((1)/(6.9* 10^5) +(1)/(2.8* 10^5) )`

`E_c=110716.332\ MPa`