A hoop, a uniform solid cylinder, a spherical shell, and a uniform solid sphere are released from rest at the top of an incline. What is the order in which they arrive at the bo…

Question

asked Dec 14, 2020 216k views

1 Answer

Eaman · Answer 1 · 2020-12-18T20:50:28+0000

Answer:

Explanation:

Given

Hoop, Uniform Solid Cylinder, Spherical shell and a uniform Solid sphere released from Rest from same height

Suppose they have same mass and radius

time Period is given by

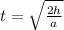$t=\sqrt{(2h)/(a)}$ ,where h=height of release

a=acceleration

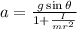
$a=(g\sin \theta )/(1+(I)/(mr^2))$

Where I=moment of inertia

a for hoop

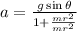
$a=(g\sin \theta )/(1+(mr^2)/(mr^2))$

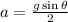
$a=(g\sin \theta )/(2)$

a for Uniform solid cylinder

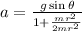
$a=(g\sin \theta )/(1+(mr^2)/(2mr^2))$

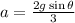
$a=(2g\sin \theta )/(3)$

a for spherical shell

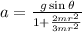
$a=(g\sin \theta )/(1+(2mr^2)/(3mr^2))$

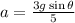
$a=(3g\sin \theta )/(5)$

a for Uniform Solid

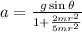
$a=(g\sin \theta )/(1+(2mr^2)/(5mr^2))$

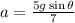
$a=(5g\sin \theta )/(7)$

time taken will be inversely proportional to the square root of acceleration

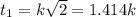
t_1=k√(2)=1.414k

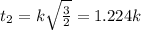
$t_2=k\sqrt{(3)/(2)}=1.224k$

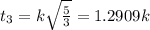
$t_3=k\sqrt{(5)/(3)}=1.2909k$

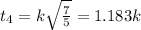
$t_4=k\sqrt{(7)/(5)}=1.183k$

thus first one to reach is Solid Sphere

second is Uniform solid cylinder

third is Spherical Shell

Fourth is hoop