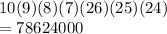Question

California has a license plate system for cars (not including trucks) where the license plate consists of 7-places. The first place is a number; the next three places are letters; and the last three places are numbers

(a) How many different California plates are possible? For example, a license plate may look different California plates are possible? For example, a license plate may loolk like 5C AA875.
(b) How many different California plates are possible if we assume that no letter or number can be repeated i a single license plate? For example, a license plate may look like 5CAR893.

Answer 1

175760000, 78624000

Explanation:

Given that California has a license plate system for cars (not including trucks) where the license plate consists of 7-places.

The first place is a number; the next three places are letters; and the last three places are numbers

a) when repitition is allowed both for numbers and letters we can have

4 numbers in 10^4 ways and 3 letters in 26^3 ways

Total no of ways =
`10^4 (26^3)`

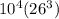
=175760000

(Because each letter can be chosen in 26 ways and each number in 10 ways)

b) If repitition is not allowed then we have to use permutations since 56 is different from 65.

4 numbers can be selected form 10 in 10P4 ways and 3 letters in 26P3 ways

Total no of ways =
`10(9)(8)(7)(26)(25)(24)\\= 78624000`