Question

1) Consider a source particle of charge qS=9 C located at (−9,5) [distances in meters]. Find the electric field vector at the target location (−15,15) [Enter the x-component in the first box, and the y-component in the second box].

2) What is the magnitude of the electric field at the target location given above?
3) What is the direction of the electric field at the target location given above? Give your answer as an angle with respect to the positive xx-direction. The angle should be between -180 degrees and 180 degrees.
4) Suppose that a particle of charge 8 C is placed at the target location. What is the electric force acting on the target particle? [Enter the xx-component in the first box, and the yy-component in the second box].
5) Calculate the total electric field at the origin due to the two charged particles from the previous problem [Enter the xx-component in the first box, and the yy-component in the second box].

Answer 1

1) E = 2.25 i^+ 0.809j^) 10⁹ N / C , 2) E = 2.39 10⁹ N / C , 3) θ = 19.8º , 4) F = 19.12 10⁹ N , 5) E = (1.32 i^+ 3.56 j^) 109 N/C

Step-by-step explanation:

1) The equation for the electric field is

E = k q / r²

Where K is the Coulomb constant that is worth 8.99 10⁹ N m² /C², q is the load and r is the distance of the load to the test point

Since the electric field is a vector magnitude, we can find its component

X axis

Ex = k q / x²

where the distance on the axis is

x = √ (X₂-x₁)²

x = √ (-15 + 9)² = 6 m

Eₓ = 8.99 10⁹ 9/6²

Eₓ = 2.25 10⁹ N /C

Y Axis

y = √ (y₂-y₁)² = √ (15-5)² = 10 m

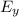`E_(y)` = 8.99 10⁹ 9/10²

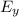`E_(y)` = 0.809 10⁹ N / C

E = Eₓ i^+
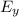`E_(y)` j^

E = 2.25 i^+ 0.809j^) 10⁹ N / C

2) the magnitude can be found using the Pythagorean triangle

E = √ (Eₓ² +
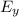`E_(y)`²)

E = √ (2.25² + 0.809²) 10⁹

E = 2.39 10⁹ N / C

3) to find the angle let's use trigonometry

tan θ =
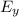`E_(y)` / Eₓ

θ = tan⁻¹
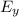`E_(y)` / Eₓ

θ = tan⁻¹ (0.809 / 2.25)

θ = 19.8º

Regarding the positive side of the x axis

4) a charge q2 = 8C is placed, let's calculate the force

F = q E

F = 8 2.39 10⁹

F = 19.12 10⁹ N

5) The total electric field at the origin, let's look for its components

q₁ = 9C

r₁ = -9 i ^ + 5 j ^

q₂ = 8 C

r₂ = -15 i ^ + 15 j ^

X axis

Eₓ = E₁ₓ + E₂ₓ

Eₓ = k q₁ / Dx₁² + k q₂ / Dx₂²

Eₓ = 8.99 10⁹ (9 / (9-0)² + 8 / (15-0)²)

Eₓ = 1.32 109 N / A

Y Axis

`E_(y)` =
`E_(1y)` +
`E_(2y)`

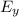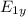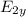
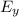`E_(y)` = k q₁ / Δy₁² + k q₂ / Δy₂²

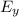`E_(y)` = 8.99 109 (9/5² + 8/15²)

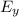`E_(y)` = 3.56 109 N / A

E = (1.32 i^+ 3.56 j^) 109 N/C