Question

A satellite of mass M moves in a circular orbit of radius R with constant speed v. True statements about this satellite include which of the following?

I) Its angular speed is v R .
II) Its tangential acceleration is zero.
III) The magnitude of its centripetal acceleration is constant.

Answer 1

We will use all three cases to define whether they are true or false.

I) The angular velocity is given as a function of the tangential velocity over the turning radius. So:

`\omega = (v)/(R)`

For the first case it is not clear if the space between the 'v' and the 'R' could have been a skipped division sign. If this sign exists, we could say that the first option is true.

II) In the linear movement if there is no change in the direction of the speed and it remains constant the acceleration will be zero, therefore

`a_T = 0`

The estate is true.

III) Centripetal acceleration is given as

`\alpha = (v^2)/(R)`

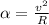
Although the speed is constant, there is a constant change in its direction, therefore the centripetal acceleration is constant, and this statement is true.