Question

Suppose p(λ) = λ(λ−1)(λ+2)(λ+1) is the characteristic polynomial of a matrix A. Consider the statements:

I: A must be a 4 × 4 matrix.
II: A can be diagonalized.
III: A is invertible.
Which of the statements I, II, and III are false?

Answer 1

Answer: The false statement is

III. A is invertible.

Step-by-step explanation: Given that the characteristic polynomial of a matrix A is

`p(\lambda)=\lambda(\lambda-1)(\lambda+2)(\lambda+1).`

We are to select the statement that is FALSE.

The characteristic values of A are given by

`p(\lambda)=0\\\\\Rightarrow \lambda(\lambda-1)(\lambda+2)(\lambda+1)=0\\\\\Rightarrow \lambda=0,1,-2,-1.`.

I. The characteristic polynomial of A has degree 4, so the order of A is 4. That is, the matrix A must be a 4 × 4 matrix.

So, the statement I is true.

II. Since all the characteristic values of A are all distinct, so there will be 4 linearly independent characteristic vectors.

Therefore, there exists an invertible matrix P such that
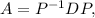`A=P^(-1)DP,` where D is daigonal with characteristic values as diagonal matrix.

This makes A diagonalizable.

So, the statement II is TRUE.

III. We know that the determinant of a matrix is equal to the product of the characteristic values of the matrix.

Therefore,

`|A|=0*1*(-2)*(-1)=0.`

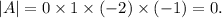
This implies that A is non-invertible.

So, statement III is FALSE.

Thus, statement III is FALSE.