Answer:
T0=390 degF
Step-by-step explanation:
The thermometer reading 70◦Fis placed in an oven preheated to a constant temperature. Through the glass window in the oven door, an observer records that the thermometer reads 110◦F after 12 minutes and 145◦F after 1 minute. How hot is the oven? Newton’s law of cooling yields the following differential equationdTdt=k(T−T0), whereT0 is the ambient temperature.
If T is temperature, then by Newton’s law
dTdt=-k(T−T0)
Where
T0− is temperature of oven
∫

ln(T-T0), from 110 to 70=-kt, from 1/2 to 0
ln(110-T0)-ln(70-T0)=-k(1/2-0)
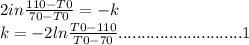
integrating the LHS of the equation from 110 to 145F
∫∫∫
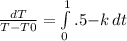
ln(145-T0)-ln(110-T0)=-k(1-1/2)
2ln145-T0/(110-T0)=-k
k=-2lnT0-145/(T0-110).......................2
couplijng equatiuon 2 with 1
(T0-110)^2=(T0-70)(T0-145)
T0^2-220T0+12100=T0^2-215T0+10150
5T0=1950
T0=390 degF