Question

Letting D D represent the maximum displacement, the extremes of the block's motion are at position A, where x = − D x=−D, and at position C, where x = D x=D. At what point in the motion is the speed of the block at its maximum?

Answer 1

The answer is at x = 0, which represents position B

Step-by-step explanation:

The full question is:

"A block is attached to a horizontal spring and set in a

simple harmonic motion, as shown from above in the figure. When the spring is relaxed, the block is a position B, where the displacement x from the equilibrium position is 0. Letting D represent the maximum displacement, the extremes of the block's motion are at position A, where x= -D, and at position C, where x= D.

At what point in the motion is the speed of the block at its maximum?"

And you can see the figure on the attached file.

Simple Harmonic motion equations

We can start from the equation that describes the position that is

`x(t)=D \sin\left(\omega t)`

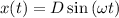
Here D stands for the amplitude which is the maximum displacement, and
`\omega` is the angular velocity, thus we can find the derivative to find the velocity equation, so we get

`v(t)=D \omega \cos (\omega t)`

And we can find the derivative again to find the acceleration.

`a(t) = -D\omega^2 \sin (\omega t)`

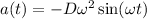
Maximum speed

We reach the maximum speed when the acceleration equation is equal to 0,

`a(t) =0\\-D\omega^2 \sin (\omega t)=0`

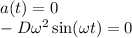
Thus it happens when

`\sin (\omega t)=0`

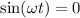
So if we replace that on the position equation we get

`x(t)=D \sin(\omega t) \\x(t)=D(0)\\x(t)=0`

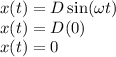
Thus the position where the speed of the block is at at its maximum is when it is going back to the origin, that is x = 0, so point b.