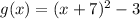Question

The function f(x) = x is translated 7 units to the left and 3 units down to form the function g(x). Which represents g(x)?

g(x) = (x-7)2 - 3
g(x) = (x + 712 - 3
g(x) = (x - 3)2 - 7
g(x) = (x-3)2 + 7
Save and Exit
Next
Mark this and return
Submit

Answer 1

Second option:
`g(x)=(x+7)-3`

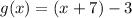
Explanation:

The exercise is actually:

"The function
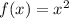`f(x) = x^2` is translated 7 units to the left and 3 units down to form the function g(x). Which represents g(x)?

`g(x) = (x-7)^2 - 3\\g(x) = (x + 7^2 - 3\\g(x) = (x - 3)^2 - 7\\g(x) = (x-3)2 + 7` "

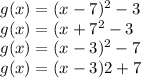Below are shown some transformations for a function f(x):

1. If
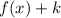`f(x)+k`, the function is shifted up "k" units.

2. If
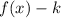`f(x)-k`, the function is shifted down "k" units.

3. If
`f(x+k)`, the function is shifted left "k" units.

4. If
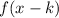`f(x-k)`, the function is shifted right "k" units.

In this case the exercise provides you the following parent function:

`f(x) = x^2`

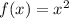
Then, keeping on mind the transformations explained before, if the given function f(x) is translated 7 units to the left and 3 units down in order to form the function g(x), then you can conclude that:

`g(x)=f(x+7)^2-3`

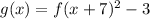
Therefore, you can determine that the function g(x) is:

`g(x)=(x+7)^2-3`