Question

The scores on an achievement test are normaly distributed with mean µ = 100 and standard deviation σ = 100. What should the score of a student be to place him or her among the top 10% of all students who tool the test?

Answer 1

the student should score atleast 229 to be among the top 10%.

Explanation:

in terms of the normal distribution, and if the table that you're using calculates the area of the normal distribution from the mean to a point x, only then what we are actually finding the value 'x' at which the z-score is at 40% (the rest 50% is already skipped by the table)

`P(0.4) = (x - \mu)/(\sigma)`

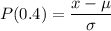
after finding the the value at this z-score, we can find the value of x at which the score is in the top 10% range.

we can find the z-score either using a normal distribution table or calculator. (but be sure what area is it calculating)

looking at the table the closest value we can find is, 0.4015 at z = 1.29 ((it is above 40% because we want to be in the top 10% range)

`P(0.4015) = (x - 100)/(100)`

`1.29 = (x - 100)/(100)`

`x = 1.29(100) + 100`

`x = 229`

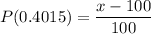
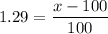
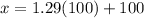
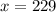
the student should score atleast 229 to be among the top 10%.