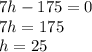Answer:
For h= 25, b in the plane spanned by a1 and a2
Explanation:
![a1= \left[\begin{array}{c}1\\2\\-1\end{array}\right] \\a2 = \left[\begin{array}{c}-7\\-7\\2\end{array}\right] \\\\b = \left[\begin{array}{c}3\\-22\\h\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/mj7nc8gt343dysy1v64iue7x8p17qubgn8.png)
we have to find value of h for which b in the plane spanned by a1 and a2.
For this the linear systems given by the following augmented matrix must be consistent.
![\left[\begin{array}cc1&-7&3\\2&-7&-22\\-1&2&h\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/q0ell7intr15rrxjzuataocjrp1xq8o589.png)
Reduce the augmented matrix into row echelon form:
![R_(2) - 2R_(1) , R_(3) + R_(1)\\\\\left[\begin{array}cc1&-7&3\\0&7&-28\\-0&-5&h+3\end{array}\right]\\\\7R_(3)+5R_(2)\\\\\left[\begin{array}cc1&-7&3\\0&7&-28\\-0&0&7h-175\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/40cuwrnjhshtc0g66q06glxc5w8y9r8rtl.png)
For system to be consistent: