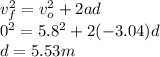Answer:
5.53 m
Step-by-step explanation:
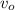 = initial speed of shuffleboard disk =
= initial speed of shuffleboard disk =
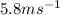
 = final speed of shuffleboard disk =
= final speed of shuffleboard disk =

 = Coefficient of kinetic friction between the disk and concrete court = 0.31
= Coefficient of kinetic friction between the disk and concrete court = 0.31
acceleration due to friction is given as
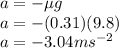
 = distance traveled by disk before it stops
= distance traveled by disk before it stops
using the kinematics equation that fits the above the data, we have