Answer:
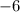 meters.
meters.
Explanation:
We have been given Mr. Mole left his burrow and started digging his way down at a constant rate.
We are also given a table of data as:
Time (minutes) Altitude (meters)
6 -20.4
9 -27.6
12 -34.8
First of all, we will find Mr. Mole's digging rate using slope formula and given information as:
 , where,
, where,
 represents difference of two y-coordinates,
represents difference of two y-coordinates,
 represents difference of two corresponding x-coordinates of y-coordinates.
represents difference of two corresponding x-coordinates of y-coordinates.
Let
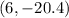 be
be
 and
and
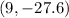 be
be
 .
.
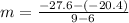
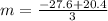
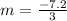
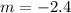
Now, we will use slope-intercept form of equation to find altitude of Mr. Mole's burrow.
 , where,
, where,
m = Slope,
b = The initial value or the y-intercept.
Upon substituting
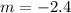 and coordinates of point
and coordinates of point
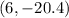 , we will get:
, we will get:
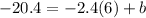



Since in our given case y-intercept represents the altitude of Mr. Mole's burrow, therefore, the altitude of Mr. Mole's burrow is
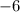 meters.
meters.