Question

Wire of length 20m is divided into two pieces and the pieces are bent into a square and a circle. How should this be done in order to minimize the sum of their areas? Round your answer to the nearest hundredth?

Answer 1

The wire must be divided into two pieces of 11.20 meters and 8.20 meters.

Explanation:

Given,

The length of the wire = 20 meters,

Let the first part of the wire = x meters,

So, the second part of the wire = (20-x) meters,

Since, by the first part of the wire, a square is formed,

if a be the side of the square,

Then 4a = x ( perimeter of a square = 4 × side ),

`\implies a =(x)/(4)`

So, the area of first part,

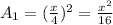`A_1=((x)/(4))^2=(x^2)/(16)` ( area of a square = side² ),

Now, by the second part of the wire, a circle is formed,

if r be the radius of the circle,

Then
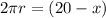`2\pi r = (20-x)` ( circumference of a circle =
`2\pi` × radius ),

`\implies r =((20-x))/(2\pi )`

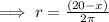
So,the area of second part,

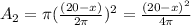`A_2=\pi (((20-x))/(2\pi ))^2=((20-x)^2)/(4\pi)` ( area of a cirle =
`\pi` × radius² ),

Thus, the total sum of areas,

`A = A_1 + A_2`

`A=(x^2)/(16)+((20-x)^2)/(4\pi)`

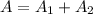
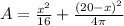
Differentiating with respect to x,

`A' = (x)/(8)-(20-x)/(2\pi)`

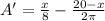
Again differentiating w. r. t. x,

`A'' = (1)/(8)+(1)/(2\pi)`

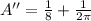
For maxima or minima,

A' = 0

`(x)/(8)-(20-x)/(2\pi)=0`

`(\pi x- 80+4x)/(2\pi)=0`

`\pi x - 80 + 4x=0`

`(\pi +4)x=80`

`\implies x =(80)/(\pi + 4)\approx 11.20`

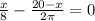
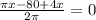
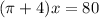
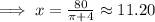
For x = 11.20, A'' = positive,

i.e. A is minimum at x = 11.20

∵ 20 - 11.20 = 8.80

Hence, the parts must be 11.20 meters and 8.80 meters in order to minimize the sum of their areas

Answer 2

The radius of the circle ,r= 1.43 m

The length of the side of square ,a= 2.77 m

Explanation:

Given that

L= 20 m

Lets take radius of the circle =r m

The total parameter of the circle = 2π r

Area of circle ,A=π r²

The side of the square = a m

The total parameter of the square = 4 a

Area of square ,A'=a²

The total length ,L= 2π r+ 4 a

20 = 2π r+ 4 a

r=3.18 - 0.63 a

The total area = A+ A'

A" =π r² +a²

A"= 3.14(3.18 - 0.63 a)² + a²

For minimize the area

`(dA`

3.14 x 2(3.18 - 0.63 a) (-0.63) + 2 a = 0

3.14 x (3.18 - 0.63 a) (-0.63) + a = 0

-6.21 + 1.24 a + a=0

2.24 a = 6.21

a=2.77 m

r= 3.18 - 0.63 a

r= 3.18 - 0.63 x 2.77

r=1.43 m

Therefore the radius of the circle ,r= 1.43 m

The length of the side of square ,a= 2.77 m