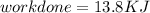Question

A 75-g bullet is fired from a rifle having a barrel 0.580 m long. Choose the origin to be at the location where the bullet begins to move. Then the force (in newtons) exerted by the expanding gas on the bullet is 18000 + 10000x - 26000x2, where x is in meter

Answer 1

The question is incomplete, below is the complete question \

"A 75g bullet is fired from a rifle having a barrel 0.580m long. Choose the origin to be at the location where the bullet begins to move. Then the force (in newtons) exerted by the expanding gas on the bullet is 18000 + 10000x - 26000x2, where x is in meter. Determine the work done by the gas on the bullet as the bullet travels the length of the barrel."

The answer is
`workdone=13.8KJ`

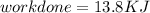
Step-by-step explanation:

From the expression of work-done, which is the product of the force and the distance, mathematically,

`work-done=force*distance`

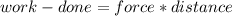
since the force in the question is dependent on the distance covered, we can integrate over the distance to get the work-done, i.e

`workdone=\int\limits^a_b {f(x)} \dx\\`

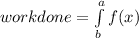
where a,b are the final distance and initial distance respectively.

From the question the force is giving as

`f(x)=18000+10000x +26000x^(2)\\`

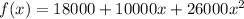
since the bullet moves through the barrel of 0.580m long and choosing the origin as the location where the bullet begins to move, our integrating point will be

`a=0.580\\b=0\\`

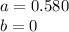
Hence, we can now write

`workdone=\int\limits^a_b {18000+10000x +26000x^(2)} \, dx`

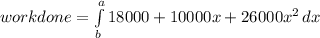
integrating the expression,we have

`[18000+5000x^(2)-(26000x^(3))/(3)]^(0.580)_(0)`

`workdone=18000(0.580)+5000(0.580)^(2)-(26000(0.580)^(3))/(3)\\workdone=10440+1682+1690.97\\workdone=13812.97J\\`

to KJ we divide the workdone by 1000, hence

`workdone=13.8KJ`