Answer: The lower bound is 0.26 and the upper bound is 0.34.
Explanation:
Formula to find the confidence interval for population proportion (p) is given by :_
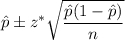
, where n= sample size
z* = Critical value. (two-tailed)
 = Sample proportion.
= Sample proportion.
Let p be the true population proportion of hits to at bats for the entire team during the last season.
As per given , we have
n= 300
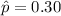
By z-table , the critical value for 90% confidence interval : z* = 1.645
Now , 90% confidence interval for the proportion of hits to at bats for the entire team during the last season:
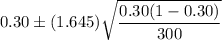
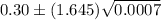

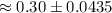
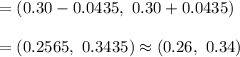
The lower bound is 0.26 and the upper bound is 0.34.