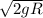Question

A block of mass m is released from rest at a height R above a horizontal surface. The acceleration due to gravity is g. The block slides along the inside of a frictionless circular hoop of radius R. Which one of the following expressions gives the speed of the block at the bottom of the hoop?

Answer 1

`v=√(2gR)\ m/s`

Step-by-step explanation:

Given that

Mass = m

Height h=R

acceleration due to gravity = g m/s²

Initially the speed of the mass ,u=0 m/s

The final speed of the mass at bottom = v m/s

Now from work power energy theorem

Work done by all forces=Change in the kinetic energy

Given that surface is friction less that is why work done by the friction force is zero.

`mgh=(1)/(2)mv^2-(1)/(2)mu^2`

`mgR=(1)/(2)mv^2`

`v=√(2gR)\ m/s`

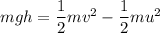
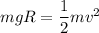
Therefore the speed at the bottom of the circular loop is
`√(2gR)`