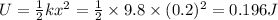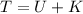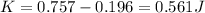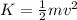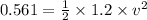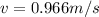Question

A horizontal spring with spring constant of 9.80 N/m is attached to a block with a mass of 1.20 kg that sits on a frictionless surface. When the block is 0.345 m from its equilibrium position, it has a speed of 0.540 m/s.(a) What is the maximum displacement of the block from the equilibrium position?m(b) What is the maximum speed of the block?m/s(c) When the block is 0.200 m from the equilibrium position, what is its speed?m/s

Answer 1

Step-by-step explanation:

Given

at certain point displacement and velocity is 0.345 m and 0.54 m/s

Therefore Potential and Kinetic Energy associated is

`U=(1)/(2)kx^2`

`U=(1)/(2)* 9.8* (0.345)^2`

`U=0.583 J`

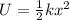
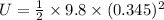
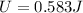
Kinetic Energy
`K=(1)/(2)mv^2`

`k=(1)/(2)* 1.2* (0.54)^2=0.174 J`

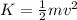
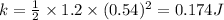
Total Energy
`T=U+K=0.583+0.174=0.757 J`

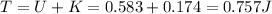
Total Energy is conserved hence at maximum displacement all energy will be Potential energy

`T=(1)/(2)kA^2`

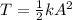
where A=maximum displacement

`0.757=(1)/(2)* 9.8* A^2`

`0.1544=A^2`

`A=0.393 m`

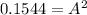
Maximum speed occurs at equilibrium Position where Potential Energy is zero

thus
`T=(1)/(2)mv^2`

`0.757=(1)/(2)* 1.2* v_(max)^2`

`v_(max)=1.123 m/s`

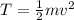
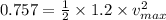
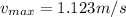
(c)When block is at 0.2 m from Equilibrium speed then its Potential Energy is

`U=(1)/(2)kx^2=(1)/(2)* 9.8* (0.2)^2=0.196 J`

`T=U+K`

`K=0.757-0.196=0.561 J`

`K=(1)/(2)mv^2`

`0.561=(1)/(2)* 1.2* v^2`

`v=0.966 m/s`