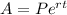Question

If $1500 is invested in a bank account at 5% interest, find the amounts present in the account at the end of 2 years if the interest is compounded:___________

(i) annually,
(ii) every 3 months,
(iii) continuously.

Answer 1

(i) $ 1653.75

(ii) $ 1653.75

(ii) $ 1657.76

Step-by-step explanation:

Since, the amount formula in compound interest,

`A=P(1+(r)/(n))^(nt)`

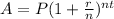
Where,

P = Principal amount,

r = annual rate of interest,

t = number of years,

n = number of compounding periods per year,

(i) P = 1500, r = 5% = 0.05, t = 2 years, n = 1,

`A=1500(1+0.05)^2 = 1500(1.05)^2 = \$ 1653.75`

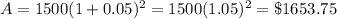
(ii) P = 1500, r = 5% = 0.05, t = 2 years, n = 4,

`A=1500(1+(0.05)/(4))^8 = 1500(1+0.0125)^8 = 1500(1.0125)^8\approx \$ 1653.75`

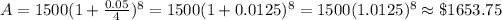
(iii) Amount formula in compound continuously,

`A=Pe^(rt)`

`A= 1500 e^(0.05* 2)=1500 e^(0.1)\approx \$ 1657.76`