) The manager of a local Gap store estimates that on average the probability of a customer entering the store and will purchase something is 20% (0.20). Assume a Binomial distri…

Question

asked Dec 11, 2020 201k views

1 Answer

Auser · Answer 1 · 2020-12-16T03:09:31+0000

Answer: 1. 0.0256

2. 0.4096

Explanation:

Binomial probability formula , to find the probability of getting x successes:

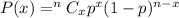P(x)=^nC_xp^x(1-p)^(n-x) , where n= Total number of trials

p= Probability of getting success in each trial.

Let x be the number of customers will make purchase.

As per given , we have

p= 0.20

n= 4

1. The probability that 3 of the next 4 customers will make a purchase will be:-

P(x=3)=^4C_3(0.20)^3(1-0.20)^(4-3)

$P(x=3)=(4)(0.20)^3(0.80)^(1)\ \ [\because\ ^nC_(n-1)=n]$

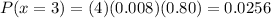
P(x=3)=(4)(0.008)(0.80)=0.0256

Hence, the probability that 3 of the next 4 customers will make a purchase = 0.0256

2. The probability that none of the next 4 customers will make a purchase will be :

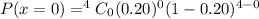
P(x=0)=^4C_0(0.20)^0(1-0.20)^(4-0)

$P(x=0)=(1)(0.80)^(4)\ \ [\because\ ^nC_(0)=1]$

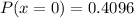
P(x=0)=0.4096

Hence, the probability that none of the next 4 customers will make a purchase= 0.4096