Question

Rampur Sarpanch requested one of his villager to donate a 6m wide land adjusted to his 132.8m long side of his right triangular plot outside the village . The other sides of the plot is 123m and 50m .On his donated land , the Sarpanch wants to construct a link road which provides the connectivity with the other villages and towns . The villager agreed at once . I) Find the area of the triangular plot remaining with the villager . Ii) What are the values involved here ?

Answer 1

Area of the remaining triangle with the villager is 1243.13 m²

Explanation:

Triangle ABC is the triangular plot of a villager shown in the figure attached.

Sarpanch requested the villager to donate land which is 6 m wide and along the side AC which measures 132.8m.

Other sides of the plot has been given as AB = 50m and BC = 123 m.

Now area of this land before donation =
`(1)/(2)* {\text{Height}}* \taxt{Base}`

=
`(1)/(2)* (123)* (50)`

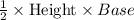
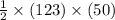
= 3075 square meter

After donation of the land the triangle formed is ΔDBE.

In ΔABC,

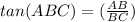
`tan(ABC)=((AB)/(BC))`

tan(∠ABC) =
`(50)/(123)`

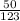
= 0.4065

∠ABC =
`tan^(-1)(0.4065)`

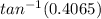
= 22.12°

In ΔEFC,

tanC =
`(EF)/(CF)`

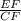
0.4065 =
`(6)/(CF)`

CF =
`(6)/(0.4065)`

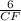
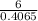
CF = 14.76 m

Since DE = AC - (CF + AG)

= 132.8 - (2×14.76)

= 132.8 - 29.52

= 102.48 m

Now in ΔDBE,

sin(∠DEB) =
`(BE)/(DE)`

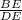
sin(22.12) =
`(BE)/(102.48)`

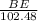
DB = 102.48×0.3765

= 38.59 m

Similarly, cos(22.12) =
`(BE)/(DE)`

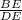
0.9264 =
`(BE)/(102.48)`

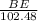
BE = 102.48×0.9264

= 94.94m

Now area of ΔDBE =
`(1)/(2)(DB)(BE)`

=
`(1)/(2)(38.59)(94.94)`

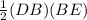
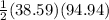
= 1831.87 square meter

Area of remaining triangle with the villager = Area of ΔABC - Area of ΔDBE

= 3075 - 1831.87

= 1243.13 square meter